É um dos vários métodos de calcular uma média.
A média harmônica dos números reais positivos a1,…,an é definida como sendo o número de membros dividido pela soma do inverso dos membros, como segue
Para o caso particular de apenas dois números, outra forma de calcular é multiplicá-los e dividir o resultado pela média aritmética dos mesmos. Matematicamente:
Utilizamos a Média Harmônica quando estamos tratando de observações de grandezas inversamente proporcionais como por exemplo, velocidade e tempo. A média harmônica é particularmente recomendada para uma série de valores que são inversamente proporcionais, como para o cálculo da velocidade média, custo médio de bens comprados com uma quantia fixa.

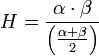
Nenhum comentário:
Postar um comentário