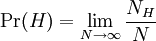Probabilidade

 A palavra probabilidade deriva do Latim probare (provar ou testar). Informalmente, provável é uma das muitas palavras utilizadas para eventos incertos ou conhecidos, sendo também substituída por algumas palavras como “sorte”, “risco”, “azar”, “incerteza”, “duvidoso”, dependendo do contexto.

Tal como acontece com a teoria da mecânica, que atribui definições precisas a termos de uso diário, como trabalho e força, também a teoria das probabilidades tenta quantificar a noção de provável.

Em essência, existe um conjunto de regras matemáticas para manipular a probabilidade, listado no tópico "Formalização da probabilidade" abaixo. (Existem outras regras para quantificar a incerteza, como a teoria de Dempster-Shafer e a lógica difusa (em inglês fuzzy logic), mas estas são, em essência, diferentes e incompatíveis com as leis da probabilidade tal como são geralmente entendidas). No entanto, está em curso um debate sobre o que é, exatamente, que as regras se aplicam; a este tópico chama-se interpretações da probabilidade.

     

Conceitos de probabilidade: A ideia geral da probabilidade é frequentemente dividida em dois conceitos relacionados:

• Probabilidade de frequência ou probabilidade aleatória, que representa uma série de eventos futuros cuja ocorrência é definida por alguns fenômenos físicos aleatórios. Este conceito pode ser dividido em fenômenos físicos que são previsíveis através de informação suficiente e fenômenos que são essencialmente imprevisíveis. Um exemplo para o primeiro tipo é uma roleta, e um exemplo para o segundo tipo é um decaimento radioativo.

• Probabilidade epistemológica ou probabilidade Bayesiana, que representa nossas incertezas sobre proposições quando não se tem conhecimento completo das circunstâncias causativas. Tais proposições podem ser sobre eventos passados ou futuros, mas não precisam ser. Alguns exemplos de probabilidade epistemológica são designar uma probabilidade à proposição de que uma lei da Física proposta seja verdadeira, e determinar o quão "provável" é que um suspeito cometeu um crime, baseado nas provas apresentadas.

 É uma questão aberta se a probabilidade aleatória é redutível à probabilidade epistemológica baseado na nossa inabilidade de predizer com precisão cada força que poderia afetar o rolar de um dado, ou se tais incertezas existem na natureza da própria realidade, particularmente em fenômenos quânticos governados pelo princípio da incerteza de Heisenberg. Embora as mesmas regras matemáticas se apliquem não importando qual interpretação seja escolhida, a escolha tem grandes implicações pelo modo em que a probabilidade é usada para modelar o mundo real.

     

   Marcos Históricos
    

O estudo científico da probabilidade é um desenvolvimento moderno. Os jogos de azar mostram que o interesse em quantificar as ideias da probabilidade tem existido por milênios, mas as descrições matemáticas de uso nesses problemas só apareceram muito mais tarde.

Cardano, no livro Liber de Ludo Aleae, estudou as probabilidades associadas ao arremesso de dados, concluindo que a distribuição de 2 dados deve ser obtida dos 36 pares ordenados de resultados, e não apenas dos 21 pares (não-ordenados).^[1]

 A doutrina das probabilidades vêm desde a correspondência entre Pierre de Fermat e Blaise Pascal (1654). Christiaan Huygens (1657) deu o primeiro tratamento científico ao assunto. A Arte da Conjectura de Jakob Bernoulli (póstumo, 1713) e a Doutrina da Probabilidade de Abraham de Moivre (1718) trataram o assunto como um ramo da matemática.

A teoria dos erros pode ser originada do Opera Miscellanea de Roger Cotes (póstumo, 1722), mas um ensaio preparado por Thomas Simpson em 1755 (impresso em 1756) foi o primeiro a aplicar a teoria na discussão de erros de observação. A reimpressão (1757) desse ensaio estabelece os axiomas que erros positivos e negativos são igualmente prováveis, e que há certos limites que se podem associar em que pode se supôr que todos os erros vão cair; erros contínuos são discutidos e uma curva de probabilidade é dada.

Pierre-Simon Laplace (1774) fez a primeira tentativa de deduzir uma regra para a combinação de observações dos princípios da teoria das probabilidades. 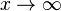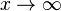Ele apresentou a lei da probabilidade dos erros por uma curva y = φ(x), x sendo qualquer erro e y sua probabilidades, e estabeleceu três propriedades dessa curva: (1) Ela é simétrica no eixo y; (2) ao eixo x, é assintótico; a probabilidade do erro quando é 0; (3) a área abaixo da curva da função é 1, sendo certo de que um erro existe. Ele deduziu uma fórmula para o significado das três observações. Ele também deu (1781) uma fórmula para a lei da facilidade de erros (um termo devido a Lagrange, 1774), mas que levava a equações não gerenciáveis. Daniel Bernoulli (1778) introduziu o princípio do produto máximo das probabilidades de um sistema de erros concorrentes.

O método dos mínimos quadrados deve-se ao matemático alemão Johann Carl Friedrich Gauss (1777-1855). Gauss descreveu o método aos dezoito anos (1795), que hoje é indispensável nas mais diversas pesquisas. Adrien-Marie Legendre (1805), introduziu contribuições ao método em seu Nouvelles méthodes pour la détermination des orbites des comètes. Por ignorar o trabalho de Legendre, um escritor Americano-Irlandês, Robert Adrain, editor de "The Analyst" (1808), primeiro deduziu a lei da facilidade do erro,

c e h sendo constantes dependendo da precisão da observação. Ele deu duas provas, sendo a segunda essencialmente a mesma de John Herschel (1850). Carl Friedrich Gauß deu a primeira prova que parece ser conhecida na Europa (a terceira após a de Adrain) em 1809. Provas posteriores foram dadas por Laplace (1810, 1812), Gauß (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), Donkin (1844, 1856), e Morgan Crofton (1870). Outros que contribuíram foram Ellis (1844), De Morgan (1864), Glaisher (1872), e Giovanni Schiaparelli (1875). A fórmula de Peters (1856) para r, o erro provável de uma observação simples, é bem conhecida.

No século XIX, os autores da teoria geral incluíam Laplace, Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion, e Karl Pearson. Augustus De Morgan e George Boole melhoraram a exibição da teoria.

No lado geométricos, (veja geometria integral), os contribuidores da The Educational Times foram influentes (Miller, Crofton, McColl, Wolstenholme, Watson, e Artemas Martin).

    

Formalização da probabilidade

Dados, símbolos da probabilidade.

   

Como outras teorias, a teoria das probabilidades é uma representação dos conceitos probabilísticos em termos formais – isso é, em termos que podem ser considerados separadamente de seus significados. Esses termos formais são manipulados pelas regras da matemática e da lógica, e quaisquer resultados são então interpretados ou traduzidos de volta ao domínio do problema.

Houve pelo menos duas tentativas com sucesso de formalizar a probabilidade, que foram as formulações de Kolmogorov e a de Cox. Na formulação de Kolmogorov, conjuntos são interpretados como eventos e a probabilidade propriamente dita como uma medida numa classe de conjuntos. Na de Cox, a probabilidade é entendida como uma primitiva (isto é, não analisada posteriormente) e a ênfase está em construir uma associação consistente de valores de probabilidade a proposições. Em ambos os casos, as leis da probabilidade são as mesmas, exceto por detalhes técnicos:

1. uma probabilidade é um número entre 0 e 1;
2. a probabilidade de um evento ou proposição e seu complemento, se somados, valem até 1; e
3. a probabilidade condicionada ou conjunta de dois eventos ou proposições é o produto da probabilidade de um deles e a probabilidade do segundo, condicionado na primeira.

    O leitor vai encontrar uma exposição da formulação de Kolmogorov no artigo sobre teoria das probabilidades, e no artigo sobre o teorema de Cox a formulação de Cox. Veja também o artigo sobre os axiomas da probabilidade.

  
Representação e interpretação de valores de probabilidade
   

A probabilidade de um evento geralmente é representada como um número real entre 0 e 1. um evento impossível tem uma probabildade de exatamente 0, e um evento certo de acontecer tem uma probabilidade de 1, mas a recíproca não é sempre verdadeira: eventos de probabilidade 0 não são sempre impossíveis, nem os de probabilidade 1 certos. A distinção bastante sutil entre "evento certo" e "probabilidade 1" é tratado em maior detalhe no artigo sobre "quase-verdade".

A maior parte das probabilidades que ocorrem na prática são números entre 0 e 1, que indica a posição do evento no contínuo entre impossibilidade e certeza. Quanto mais próxima de 1 seja a probabilidade de um evento, mais provável é que o evento ocorra. Por exemplo, se dois eventos forem ditos igualmente prováveis, como por exemplo em um jogo de cara ou coroa, podemos exprimir a probabilidade de cada evento - cara ou coroa - como "1 em 2", ou, de forma equivalente, "50%", ou ainda "1/2".

Probabilidades também podem ser expressas como chances (odds). Chance é a razão entre a probabilidade de um evento e à probabilidade de todos os demais eventos. A chance de obtermos cara, ao lançarmos uma moeda, é dada por (1/2)/(1 - 1/2), que é igual a 1/1. Isto é expresso como uma "chance de 1 para 1" e é freqüentemente escrito como "1:1". Assim, a chance a:b para um certo evento é equivalente à probabilidade a/(a+b).

Por exemplo, a chance 1:1 é equivalente à probabilidade 1/2 e 3:2 é equivalente à probabilidade 3/5.Ainda fica a questão de a quê exatamente pode ser atribuído uma probabilidade, e como os números atribuídos podem ser usados; isto é uma questão de interpretações de probabilidade.

 Há alguns que alegam que pode-se atribuir uma probabilidade a qualquer tipo de proposição lógica incerta; esta é a interpretação bayesiana. Há outros que argumentam que a probabilidade só é aplicada apropriadamente a proposições que relacionam-se com sequências de experimentos repetidos, ou da amostragem de uma população grande; esta é a interpretação frequentista. Há ainda diversas outras interpretações que são variações de um ou de outro tipo.

   
Distribuições
    

A distribuição da probabilidade é uma função que determina probabilidades para eventos ou proposições. Para qualquer conjunto de eventos ou proposições existem muitas maneiras de determinar probabilidades, de forma que a escolha de uma ou outra distribuição é equivalente a criar diferentes hipóteses sobre os eventos ou proposições em questão.

Há várias formas equivalentes de se especificar uma distribuição de probabilidade. Talvez a mais comum é especificar uma função densidade da probabilidade. Daí, a probabilidade de um evento ou proposição é obtida pela integração da função densidade.

A função distribuição pode ser também especificada diretamente. Em uma dimensão, a função distribuição é chamada de função distribuição cumulativa. As distribuições de probabilidade também podem ser especificadas via momentos ou por funções características, ou por outras formas. Uma distribuição é chamada de distribuição discreta se for definida em um conjunto contável e discreto, tal como o subconjunto dos números inteiros; ou é chamada de distribuição contínua se tiver uma função distribuição contínua, tal como uma função polinomial ou exponencial. A maior parte das distribuições de importância prática são ou discretas ou contínuas, porém há exemplos de distribuições que não são de nenhum desses tipos. Dentre as distribuições discretas importantes, pode-se citar a distribuição uniforme discreta, a distribuição de Poisson, a distribuição binomial, a distribuição binomial negativa e a distribuição de Maxwell-Boltzmann. Dentre as distribuições contínuas, a distribuição normal, a distribuição gama, a distribuição t de Student e a distribuição exponencial.

   
Probabilidade na Matemática
 

Os axiomas da probabilidade formam a base para a teoria da probabilidade matemática. O cálculo de probabilidades pode ser frequentemente determinado pelo uso da análise combinatória ou pela aplicação direta dos axiomas. As aplicações da probabilidade vão muito além da estatística, que é geralmente baseada na ideia de distribuições de probabilidade e do teorema do limite central.

Para dar um significado matemático à probabilidade, considere um jogo de cara ou coroa. Intuitivamente, a probabilidade de dar cara, qualquer que seja a moeda, é "obviamente 50%"; porém, esta afirmação por si só deixa a desejar quanto ao rigor matemático - certamente, enquanto se pode esperar que, ao jogar essa moeda 10 vezes, teremos 5 caras e 5 coroas, não há garantias de que isso ocorrerá; é possível, por exemplo, conseguir 10 caras sucessivas. O que então o número "50%" significaria nesse contexto?

Uma proposta é usar a lei dos grandes números. Neste caso, assumimos que é exequível fazer qualquer número de arremessos da moeda, com cada resultado sendo independente - isto é, o resultado de cada jogada não é afetado pelas jogadas anteriores. Se executarmos N jogadas, e seja N_H o número de vezes que a moeda deu cara, então pode-se considerar, para qualquer N, a razão N_H/N.

Quando N se tornar cada vez maior, pode-se esperar que, em nosso exemplo, a razão N_H/N chegará cada vez mais perto de 1/2. Isto nos permite "definir" a probabilidade Pr(H) das caras como o limite matemático, com N tendendo ao infinito, desta sequência de quocientes:

Na prática, obviamente, não se pode arremessar uma moeda uma infinidade de vezes; por isso, em geral, esta fórmula se aplica melhor a situações nas quais já se tem fixada uma probabilidade a priori para um resultado particular (no nosso caso, nossa convenção é a de que a moeda é uma moeda "honesta"). A lei dos grandes números diz que, dado Pr(H) e qualquer número arbitrariamente pequeno ε, existe um número n tal que para todo N > n,

Em outras palavras, ao dizer que "a probabilidade de caras é 1/2", queremos dizer que, se jogarmos nossa moeda tantas vezes o bastante, eventualmente o número de caras em relação ao número total de jogadas tornar-se-á arbitrariamente próximo de 1/2; e permanecerá ao menos tão próximo de 1/2 enquanto se continuar a arremessar a moeda.

Observe que uma definição apropriada requer a teoria da medida, que provê meios de cancelar aqueles casos nos quais o limite superior não dá o resultado "certo", ou é indefinido pelo fato de terem uma medida zero.O aspecto a priori desta proposta à probabilidade é algumas vezes problemática quando aplicado a situações do mundo real. Por exemplo, na peça Rosencrantz e Guildenstern estão mortos, de Tom Stoppard, uma personagem arremessa uma moeda que sempre dá caras, uma centena de vezes. Ele não pode decidir se isto é apenas um evento aleatório - além do mais, é possível, porém improvável, que uma moeda honesta pudesse dar tal resultado - ou se a hipótese de que a moeda é honesta seja falsa.

    
Notas sobre cálculos de probabilidade
   

A dificuldade nos cálculos de probabilidade se relacionam com determinar o número de eventos possíveis, contar as ocorrências de cada evento, contar o número total de eventos. O que é especialmente difícil é chegar a conclusões que tenham algum significado, a partir das probabilidades calculadas. Uma piada sobre probabilidade, o problema de Monty Hall, demonstra as armadilhas muito bem.

    
Aplicações da Teoria da Probabilidade no cotidiano
   

Um efeito maior da teoria da probabilidade no cotidiano está na avaliação de riscos e no comércio nos mercado de matérias-primas. Governos geralmente aplicam métodos de probabilidade na regulação ambiental onde é chamada de "análise de caminho", e estão frequentemente medindo o bem-estar usando métodos que são estocásticos por natureza, e escolhendo projectos com os quais se comprometer baseados no seu efeito provável na população como um todo, estatisticamente. De fato, não é correto dizer que estatísticas estejam envolvidas na modelagem em si, dado que, normalmente, estimativas de risco são únicas (one-time) e, portanto, necessitam de modelos mais fundamentais como, por exemplo, para determinar "a probabilidade de ocorrência de outro atentado terrorista como o de 11 de setembro em Nova York". Uma lei de números pequenos tende a se aplicar a todas estas situações e à percepção dos efeitos relacionados a tais situações, o que faz de medidas de probabilidade uma questão política.

Um bom exemplo é o efeito nos preços do petróleo da probabilidade percebida de qualquer conflito mais abrangente no Oriente Médio - o que contagia a economia como um todo. A estimativa feita por um comerciante de comodidades de que uma guerra é mais (ou menos) provável leva a um aumento (ou diminuição) de preços e sinaliza a outros comerciantes aquela opinião. Da mesma forma, as probabilidades não são estimadas de forma independente nem, necessariamente, racional. A teoria de finança comportamental surgiu para descrever o efeito de tal pensamento em grupo (groupthink) na definição de preços, política, paz e conflito.

Uma aplicação importante da teoria das probabilidades no dia-a-dia é a questão da confiabilidade. No desenvolvimento de muitos produtos de consumo, tais como automóveis e eletro - eletrônicos, a teoria da confiabilidade é utilizada com o intuito de se reduzir a probabilidade de falha que, por sua vez, está estritamente relacionada à garantia do produto. Outro bom exemplo é a aplicação da teoria dos jogos, uma teoria rigorosamente baseada na teoria das probabilidades, à Guerra Fria e à doutrina de destruição mútua assegurada.

Em suma, é razoável pensar que a descoberta de métodos rigorosos para estimar e combinar probabilidades tem tido um impacto profundo na sociedade moderna. Assim, pode ser de extrema importância para muitos cidadãos compreender como estimativas de chance e probabilidades são feitas e como elas contribuem para reputações e decisões, especialmente em uma democracia.

Correlação Linear

Correlação Linear Simples: É a análise de correlação que mede o grau de relacionamento entre as variáveis, a qual diz respeito à medida entre X e Y.
Hipóteses:
a. a relação entre X e Y é linear;
b. ambas são variáveis aleatórias;
c. homocedasticidade;
d. as distribuições condicionais de Y dado X têm distribuição Normal;
e. as duas distribuições, de X e de Y, têm distribuição Normal na população.
 Coeficiente de Determinação
2ρ- coeficiente de determinação na população
r2 - coeficiente de determinação na amostra
O coeficiente de determinação para a amostra é:
Amostra:

**Utilizando a Hp para resolver: Inserir o primeiro valor de y, enter, em seguida inserir o primeiro valor de x e depois  Σ + dando continuidade aos demais valores em seguida apertar clx 0 g 1 depois x><y       

Regressão Linear

Regressão Linear Simples: é um método para se estimar a condicional (valor esperado) de uma variável y, dados os valores de algumas outras variáveis x.
A regressão, em geral, trata da questão de se estimar um valor condicional esperado.
A regressão linear é chamada "linear" porque se considera que a relação da resposta às variáveis é uma função linear de alguns parâmetros. Os modelos de regressão que não são uma função linear dos parâmetros se chamam modelos de regressão não-linear.

Equação: y = β0+ β1. x , onde βo e β1, são respectivamente, o intercepto e a
inclinação da reta e recebem o nome de coeficientes de
regressão.
β1= xy'-x'.y' 
         x'²-x''²    
 β0= y'- β1.x' 

  * Obs.: A fórmula não está correta, pois não conseguimos fazer exatamente igual.

Moda:
Amodal – sem moda, sem valores repetidos
Ex.: X = (1,2,3)

Unimodal – Um único nº repetido
Ex.: X = (1,5,1,3)

Bimodal – Dois nº Repetidos
Ex.: X = (1,3,1,3,9)

Multimodal – Mais de 3 nº repetidos
Ex.: X = (1,3,4,1,3,4,9)

**OBS.: X = ( 1,1,2,2,3,3) Não é considerado Moda

Mediana:
Para a seguinte população:

1, 3, 5, 7, 9
A mediana é 5 (igual à média)
No entanto, para a população:
1, 2, 4, 10, 13
A mediana é 4 (enquanto a média é 6)
Para populações pares:
1, 2, 4, 7, 9, 10
A mediana é (4+7)/2, que é 5.5.

Média geométrica: Entre n valores, é a raiz de índice n do produto desses valores. Veja no exemplo, a média geométrica entre 1, 2 e 4:

Média Harmônica: A média harmônica equivale ao inverso da média aritmética dos inversos de n valores. Parece complicado, mas é bastante simples, veja o exemplo:

Média harmônica entre 2, 6 e 8. Primeiramente é necessário calcular a média aritmética dos inversos dos valores dados:

depois, faz-se o inverso do resultado, tendo finalmente as médias: 2,6,8:

Em todas as médias o resultado estará entre o maior e o menor número dado.

Para os mesmos valores, a média aritmética terá o maior valor, seguida da média geométrica e depois a média harmônica.

Exemplos das médias

Média aritmética simples

1- João deseja calcular a média das notas que tirou em cada uma das quatro matérias a seguir. Calcule a média ponderada de suas notas, sendo que as duas primeiras provas valem 2 pontos e as outras duas valem 3 pontos:

Inglês

1ª prova 6,5

2ª prova 7,8

3ª prova 8,0

4ª prova 7,1


(13 + 15,6 + 24 + 21,3) / 10 = 73,9 / 10 = 7,39


2- Calcule a média aritmética simples em cada um dos seguintes casos:

a) 15; 48 ; 36 (15 + 48 + 36) /3 = 99 / 3 = 33

b) 80 ; 71 ; 95 ; 100 (80 + 71 + 95 + 100) / 4= 346 / 4 = 86,5

c) 59 ; 84 ; 37 ; 62 ; 10 (59 + 84 + 37 + 62 + 10) / 5= = 252 / 5 = 50,4



Média aritmética ponderada


Neste tipo de média aritmética, cada número que fará parte da média terá um peso. Este peso será multiplicado pelo número, que serão somados e dívidas depois pela soma dos pesos. Veja o exemplo:

1- calcule a media aritmética ponderada dos dados citados abaixo dos atletas olímpicos:

 Mediana: é uma medida de tendência central, um número que caracteriza as observações de uma determinada variável de tal forma que este número (a mediana) de um grupo de dados ordenados separa a metade inferior da amostra, população ou distribuição de probabilidade, da metade superior. Mais concretamente, 1/2 da população terá valores inferiores ou iguais à mediana e 1/2 da população terá valores superiores ou iguais à mediana.



A mediana pode ser calculada para um conjunto de observações ou para funções de distribuição de probabilidade.



**Cálculo da mediana para dados ordenados:


No caso de dados ordenados de amostras de tamanho n, se n for ímpar, a mediana será o elemento central (N+1)/2. Se n for par, a mediana será o resultado da média simples entre os elementos e N/2 E N/2+1